Sinopsis
I – Antecedents
According to Galileo’s Relativity Principle, laws in physics are identical in any inertial reference system. The Classical Mechanics, and even most of the modern theories in physics, have been formulated for inertial reference frames, checking their validity in those systems.
Out of these limits there are other assumptions in nature, for which we nowadays still ignore the laws of their behaviour. One example is the analysis of bodies equipped with rotational movement, because in their case it is necessary to take into account the inertial reactions which might happen.
Several experimental references infer the existence of a different rotational dynamics, non-Newtonian, necessary for the identification of the behaviour of rotating bodies, when exposed to new non-coaxial stimuli, and the behaviour of which, in many cases nowadays, is considered as paradoxical or chaotic, because the laws that we dispose of do not allow to identify and predetermine it.
II- Deduction
This new non inertial and non-Newtonian rotational dynamics can be inferred at least in two differentiated ways:
- Relativistic deduction.
- Non relativistic deduction.
Relativistic deduction. Abstractly, one can mathematically infer a system of equations, which allow the comprehension of the fundamental interactions generated in nature. These equations show how the matrix of a tetra-dimensional rotation of a reference frame is associated with the inertial field Tijk originated by the rotation, and new motion equations can be deduced, hence a general expression of the motion equations in the gravitation theory of Einstein.
Non relativistic deduction. In the assumptions of simultaneous non coaxial rotations the rigid body experiences non-homogeneous speed fields. Said fields with non-homogeneous distributions, generate anisotropic acceleration fields. These fields can be interpreted as fields of inertial forces, created in space through the effect of simultaneous non coaxial rotations.
Based on the expressed, we can interpret that the gyroscopic momentum does not exist physically, as it simply is the observable effect of a field of inertial forces generated by the simultaneous, non-coaxial, rotation of space. This phenomenon might get structured in a new rotational dynamic of non inertial systems, within the scope of the Theory of Dynamic Interactions.
Based on the Principle of Conservation of the Motion quantity, the gyroscopic momentum under observation will be equivalent to the one acting from the outside. Therefore we can infer that the field of inertial forces generated in the rotating space by a new non coaxial momentum M´, upon a moving body with a rotational movement 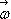 and an inertial momentum I upon that rotation axis, and, thus, with an angular momentum L , will oblige the moving body to acquire a precession speed
and an inertial momentum I upon that rotation axis, and, thus, with an angular momentum L , will oblige the moving body to acquire a precession speed 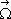 .
.
This precession speed 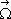 can be observed simultaneously with the initial
can be observed simultaneously with the initial ![]() , which remains constant within the body. Further, and as discriminating hypothesis in the case of transfer movement of the body, we propose the dynamic hypothesis which says that the transfer speeds’ field couples to the anisotropic field of inertial speeds created by the second non-coaxial momentum, obtaining as result an orbiting movement, which is simultaneous with the intrinsic rotation of the moving body. This new orbiting movement, generated by a non-coaxial momentum, is defined by the rotation of the speed vector, the latter staying constant in module. As motion equation we obtain:
, which remains constant within the body. Further, and as discriminating hypothesis in the case of transfer movement of the body, we propose the dynamic hypothesis which says that the transfer speeds’ field couples to the anisotropic field of inertial speeds created by the second non-coaxial momentum, obtaining as result an orbiting movement, which is simultaneous with the intrinsic rotation of the moving body. This new orbiting movement, generated by a non-coaxial momentum, is defined by the rotation of the speed vector, the latter staying constant in module. As motion equation we obtain:
Where is the matrix which represents the rotation in space of the speed vector. So we can associate dynamic effects to the speed, and a clear mathematical correlation between rotation and transfer. This mathematical correlation allows us to identify a physical relation between transfers of kinetic rotational energy to kinetic transfer energies, and vice-versa.
Quite a number of examples can be thought of for checking these dynamic hypotheses, which would allow us to interpret many assumptions in nature, which still remain unexplained up to date. This new Non-inertial Rotational Dynamics based on the Theory of Dynamic Interactions, is developed in laws and corollaries, allowing a number of new, unknown scientific and technological applications.
III – Generalization of the inertial phenomena
As we expressed in the beginning, the classical mechanics has been formulated for inertial reference frames, and not for rotating spaces of events. Nevertheless, it is possible to think of a new mechanics for any type of space, adding their inertial reactions and defining a dynamics of inertial fields. Thus, the inertial phenomena would also become structured in a rational way, and get incorporated into a unified mechanics. In order to incorporate the inertial phenomena into the structure of physical knowledge, it is necessary to analyze the motion in non-holonomous coordinates and the resulting axial reactions, in the understanding that a mechanics such as the classical mechanics, based on holonomous coordinates and polar reactions, will only represent a limited and partial view of nature.
The proposed generalization does not say that classical mechanics is obsolete or wrong, but simply that it is partial and limited, as it refers to the specific assumption of inertial systems. We wish and are able to be more ambitious, looking for more general dynamic laws, aiming to establish the behaviour of moving bodies when rotating, or even when they are exposed to multiple non-coaxial rotations of the space of events, and which allow us to predetermine the inertial reactions that will occur and their true dynamic effects.
We understand that the Theory of Dynamic Interactions incorporates and represents the generalization of the inertial behaviour of the matter, but at the same time it could be generalized by a conceptually wider relativity theory, allowing a unified structure of the physical knowledge.
IV –Scientific significance
The Theory of Dynamic Interactions generalizes the concept of gyroscopic momentum and of other inertial phenomena, incorporating them into the unified structure of a new rotational dynamics of non inertial systems. According to the defended Theory of Dynamic Interactions, we can conceive a universe in constant dynamic balance, in which a force momentum, with a zero resultant, will as long as it works generate a movement of constant orbiting, within a closed path. The importance of this mathematical model is obvious, in which not only the forces are leading players, but also the momentums of forces which, while staying constant, will generate orbiting and constantly recurrent movements, generating a system in dynamic balance, and not in unlimited expansion.
This new dynamics theory will lend us a better understanding of how universe and matter behave. It will generate numerous technological applications, such as the steering of space ships, energetic applications by means of designing a dynamic lever, the more precise calculation of ballistic paths, of trajectories of satellites or of space probes, or even the determination of the devastating effect of hurricanes. To end, we can remember Rule I, of Book III of The Mathematical Principles of Natural Philosophy, by Isaac Newton: “We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances.”
The Theory of Dynamic Interactions is reasoned out and described in the newly published book of Gabriel Barceló:
Un Mundo en Rotación (2008), and its antecedents and fundamentals are enunciated in the book of the same author: El Vuelo del Bumerán (2005).
